巡回冗長検査(CRC, Cyclic Redundancy Check)の原理と実装

実務でCRC、巡回冗長検査を使うことがあったのですが、いまいちよくわかっていなかったので調べてみました。間違いあれば訂正します。

CRCとは
使い始めるために
補足説明あれこれ
- 実装都合の知識
- CRCの特性
まとめ
参考

CRCとは

wikipediaの引用です。

巡回冗長検査（じゅんかいじょうちょうけんさ、英: Cyclic Redundancy Check, CRC）は、誤り検出符号の一種で、主にデータ転送などに伴う偶発的な誤りの検出によく使われている。送信側は定められた生成多項式で除算した余りを検査データとして付加して送信し、受信側で同じ生成多項式を使用してデータを除算し、その余りを比較照合することによって受信データの誤り・破損を検出する。

巡回冗長検査 - Wikipedia

生成多項式 $G(x)$ を使用して送信するメッセージから検査データを作り、それを付加して送信します。受信側は受信したメッセージから検査データを作り、付加された検査データと比較して受信データの誤りを検出する仕組みです。

検査データには生成多項式による剰余を利用しています。厳密な数学(情報工学)の定義を抜きにすると、以下サイトの説明がわかりやすいです。CRCの根本的な考え方が書かれています。

http://funini.com/kei/math/crc_basic.shtml

使い始めるために

「CRCを実装してください」と言われたら、少なくとも以下が決まれば実装して使い始めることができます。

生成多項式
ビットシフト方向
初期値
出力(除算結果)のXOR反転パターン

生成多項式以外は、実装上の都合からくるものなので一旦おいておきます。CRCを(アイディア的な意味で)理解するためには最低限、生成多項式と二元系列での除算について知っておく必要があります。

生成多項式

生成多項式は、仕様上では以下のように指定されていたりします。

$G(x) = x^ 4 + x^ 2 + x^ 1 + 1$

CRCを扱う上では、二元系列の多項式表現という表現を使います。0, 1を成分とするベクトル ${\boldsymbol{v} = (v_{n-1}, v_{n-2}, ... , v_{0} ) }$ は二元系列の多項式表現では以下のようになります。

$F(x) = v_ {n-1}x^ {n-1} + v_ {n-2}x^ {n-2} + ... + v_ 0$

変数 $x$ に大きな意味はありません。単に係数を区別するためのものです。CRCの計算では、この多項式の係数となる $\boldsymbol{v}$ が使われます。先に上げた生成多項式は0, 1で表すと10111となります。(実際に使われる生成多項式はもっと長いですが、簡単のため短くしています)

二元系列での除算

難しいことは抜きにして説明すると、二元系列での除算はXORの繰り返しで実現されます。

例えば10010101を10111で割る場合、以下のような計算になります。

f:id:gco46:20201108134701p:plain

剰余は11となりました。多項式で書くと、

$\displaystyle (x^7 + x^4 + x^2 + 1) = (x^3 + x)(x^4 + x^2 + x + 1) + (x + 1)$

$(x^3 + x)$ が商、 $(x+1)$ が剰余です。二元系列での演算はmod2で行われているため、違和感はありますがこれで正しいです。

CRCの計算

では実際に0x31B6というメッセージのCRCを計算してみます。これを二進数に直すと0011000110110110です。

計算は以下の手順で行われます。

生成多項式の次数だけ、メッセージの右側に0を加える
ひたすらXORして剰余を求める

生成多項式は $G(x) = x^{4} + x^2 + x + 1$ を使用します。次数は4なので、4つ0を右につけます。計算は以下です。

f:id:gco46:20201108134727p:plain

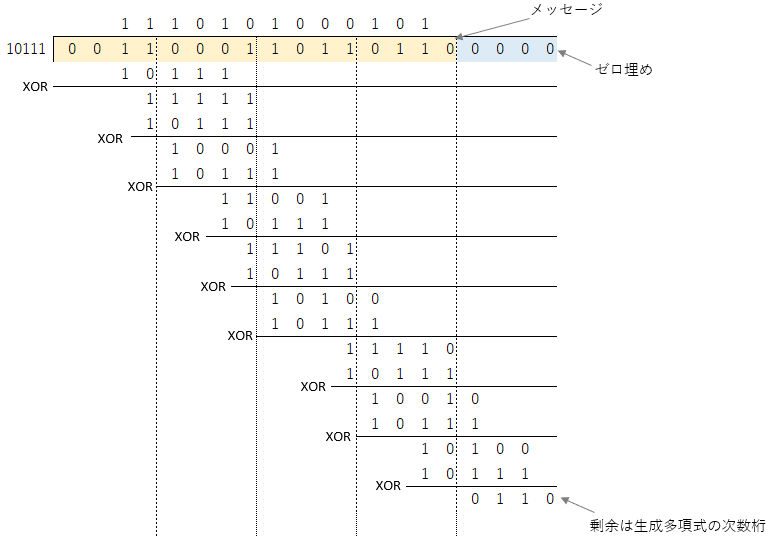
これにより、0x31B6のCRC検査データは0110となります。検査データのビット数は生成多項式の次数と等しくなります。検査データを多項式表現すると $(m-1)$ 次式となるので、次数 $m$ の多項式の剰余としては納得できる結果であると思います。

最初にメッセージの右側を0で埋めるのは、メッセージがそのままCRCとなるのを防ぐためです。CRCは任意のデータ長の検査データを作ることができますが、メッセージが $(m-1)$ 次だった場合、次数 $m$ の生成多項式による剰余はそのままメッセージと等しくなってしまいます。（CRCが理論的に保証する性能を担保することができなくなります）

実装

以上より、CRCのアイディアは説明されました。実装するにはまだ足りませんが、「なんかよくわからない検査ビットをくっつける」というレベルからは脱したと思います。

ここで、上記ケースCRCを計算するための実装例(python)を紹介します。 $G(x) = x^4 + x^2 + x + 1$ を使った実装(便宜的にCRC4と名付けます)は以下です。

def make_crc4(message):
    # CRC計算結果(初期値は0000)
    crc = 0b0000
    # 生成多項式
    poly = 0b0111
    
    for i in range(len(message)):
        # データの逐次投入
        crc = crc ^ (message[i])
        for j in range(4):
            if (crc & 0b1000 == 0b1000):
                # 先頭ビットが1ならXOR
                # 左ビットシフト
                crc = poly ^ (crc << 1)
            else:
                crc = (crc << 1)

    # crcの下位4bitのみ使用（python特有の処理）
    return crc & 0b1111

# 0x31B6
# データの逐次投入のために、4bitずつに分割
data = [0b0011, 0b0001, 0b1011, 0b0110] 
crc4 = make_crc4(data)
print(bin(crc4))

(return crc & 0b1111は動的型付けであるpython特有の処理なので気にしなくて良いです。そもそもpython使うなって話ですが…)

例で挙げたCRCの計算は最もシンプルで、

初期値==0
左ビットシフト
出力のXOR反転パターン==0000

での計算と等価です。実運用ではCRC計算を回路で実現することも多いので、ハードウェア実装の都合で仕様が決められたりします。規格として仕様が決められているものはググれば実装がすぐ出てくるので、CRCのアイディアだけ理解しておけばコピペで済みます。例えばCRC16-IBMのCによる実装は以下です。

http://www.soramimi.jp/crc16/

補足説明あれこれ

実装都合の知識

CRCのの根幹アイディアとググって出てくる実装例には乖離がありすぎるため、理解が難しいです。ここではその理解の助けになれるように知識を補完します。

生成多項式の先頭ビット省略

$G(x) = x^4 + x^2 + x + 1$ は10111となるはずですが、上の実装ではpoly = 0111となっています。除算をする場合、先頭の1はXORで必ず消えるため、「被除数の先頭ビットが1かどうかのみ確認し、1だったら $G(x)$ の $(m-1)$ 次以下の成分のXORを取る」という処理に置き換えられます。

f:id:gco46:20201108145241p:plain

「1ビットくらいいいじゃん」と思うかもしれませんが、実際のCRCは生成多項式の次数が32次とかにもなりえます。その1ビットのせいで4byteに収まらなくなるのは、リソース制約がある実務環境では嬉しくありません。

データの逐次投入

実装例で一番不思議に思うのが、crc = crc ^ message[i]の部分かと思います(自分はそうでした)。これはXOR演算に交換法則が成り立つことを利用した実装です。

CRCの根幹アイディアの通り愚直に実装しようとすると、（メッセージ+生成多項式の次数）ビットのデータを格納するための変数を用意する必要があります。実用上(イーサネットの規格など)では10000bitとかのメッセージに対してCRCを計算しますが、愚直実装では不可能なのが明らかです。そこでメッセージを小さい単位に分割して処理することを考えます。

CRCは結局の所、XOR演算の中で各桁に何回1が現れるかとカウントすれば良いので、厳密にはCRCの検査ビット数分だけの変数を用意しておけばよいです。このへんは言葉では説明しにくいですね…

f:id:gco46:20201108145255p:plain

この方法を利用すれば、計算に使用するRAM容量は一定のままで任意長のメッセージのCRCを計算できます。上の実装例ではCRC計算結果が4bitなので、4bitずつメッセージを読み込んでいます。実際には後で述べるテーブル参照を利用するために、1byte単位で読み込むことが多いです。

初期値の反転

データの逐次投入より、CRC結果を格納するための変数さえ用意すれば良いことがわかりました。実用上ではそのCRCの初期値を反転（全て1）させて計算する事が多いです。これはおそらくハードウェア実装に依存する問題です（調べましたが明確な理由は見つからなかったです…）。「全0のメッセージに対してのCRCが0になり、レジスタ値が全0になる故障が検出できなくなるのを防ぐため」という説が有力そうです。

XORの交換法則より、1が現れる回数が変わるだけなので通常時の演算は本質的には変わりません。

出力のXOR反転パターン

計算結果のCRCを決められたパターンのbit列とXORを取るだけです。0xFFFFとかが使われたりします。初期値の反転を実施した上で出力を全反転させると、結果的には反転が帳消しになります。これもおそらくハード実装の都合で決められる部分かと思います。

ビットシフト方向

演算時のビットシフトの方向を指定します。例では左シフトを挙げましたが、右シフトではビット順を反転させて計算します。すなわち、メッセージを

0011000110110110 (0x31B6)
 ↓
0110110110001100 (0x6D8C)

として右にビットシフトさせながら計算します。もちろん生成多項式も反転します。

ビットシフトは通信やハードの都合で決められます。LSBから伝送されるシリアル通信やプロセッサのエンディアンによって右ビットシフトが選択されるっぽいです。

テーブル参照

計算を高速化するためにテーブル参照という方法が取られることがあります。以下にCによるCRC16の実装を載せます。

unsigned short crc16(unsigned short crc, unsigned char const *ptr, int len)
{
#define CRC16POLY 0xa001
    int i, j;
    crc = ~crc;
    for (i = 0; i < len; i++) {
        crc ^= ptr[i];
        for (j = 0; j < 8; j++) {
            if (crc & 1) {
                crc = (crc >> 1) ^ CRC16POLY;
            } else {
                crc >>= 1;
            }
        }
    }
    return ~crc;
}

引用元：http://www.soramimi.jp/crc16/

python実装例でもそうでしたが、二重ループが含まれています（データ逐次投入のループ i と、ビットシフトのループ j ）。逐次処理するデータの単位が1byteと決まっていれば、予め1byteで表現できる256通り分のCRC計算をしておいたテーブルを作成することで、ビットシフトのループをなくすことができます。詳細な実装例は上の引用元サイトで見ることができます。

当然ですが、テーブル参照方式ではROMの容量を消費するためリソースとは要相談です。 $2^8$ 通り、つまり256通りx 2byte = 512byteくらいがテーブルの現実的なサイズになるので、自ずとデータ逐次投入の単位も1byteとなる事が多いようです。

CRCの特性

端的に言うと、CRCはバースト誤りに対する強力な検出性能を持つことが理論的に保証されています。これが他の誤り検出（水平垂直パリティ検査符号やハミング符号）とは異なるCRCの特性です。バースト誤りとは、「長さ $n$ のメッセージ中で長さ $l (\lt n )$ の連続した誤りが一回起こること」です。これに対して、断続的に発生する誤りをランダム誤りと呼びます。

$m$ 次の生成多項式を使用した時、長さ $m$ の区間内でのバースト誤りは全て検出可能です。また、生成多項式の選び方によりますがCRC-CCITTという規格の場合は(一定長以下のメッセージなら)3bitまでの任意のランダム誤りが検出できます。バースト誤りの証明は意外と単純なので興味があれば調べてみてください。以下の資料が参考になります。

http://www-ikn.ist.hokudai.ac.jp/~kida/lecture/IT_14.pdf

数学的な背景は以下サイトが参考になるかもしれません。

qiita.com

注意点として、生成多項式は適切なものを選ぶ必要があります。生成多項式は周期と呼ばれる数値を持っており、（メッセージ長 + CRC検査ビット長）が周期以下とならなければ誤り訂正能力が保証されません。例で挙げたCRC4の生成多項式の周期は7であるため、実際には誤り訂正できません(1bit誤り検出は可能)。大体は規格で決められているものを使うため問題になることはないと思います。ちなみにCRC-CCITTの周期は32767だそうです。